Wprowadzenie
Analiza ryzyka w korporacjach przestała być dodatkiem do planowania, a stała się jego fundamentem. Firmy działające w środowisku pełnym niepewności muszą przewidywać nie tylko najbardziej prawdopodobny scenariusz, ale również to, co może wydarzyć się na skrajach rozkładu. I właśnie tutaj pojawia się analiza Monte Carlo, narzędzie, które zrewolucjonizowało podejście do oceny ryzyka i tworzenia prognoz finansowych. Dzięki niej zarządy korporacji przestały patrzeć na świat w sposób czarno-biały, a zaczęły widzieć jego pełne spektrum od skrajnie pesymistycznego po nadzwyczaj optymistyczny.
Monte Carlo pozwala na symulowanie tysięcy możliwych wyników, co daje obraz ryzyka znacznie bardziej realistyczny niż tradycyjne metody oparte na jednym scenariuszu. W dużych firmach stosuje się ją zarówno w procesach inwestycyjnych, jak i w budżetowaniu, planowaniu strategicznym czy ocenie wartości przedsiębiorstwa. Co ciekawe, coraz częściej analitycy wykonują te symulacje bez specjalistycznego oprogramowania tylko wystarczy im Excel oraz kilka sprytnie zastosowanych formuł.
W tym artykule przedstawiam, jak działa Monte Carlo, dlaczego stała się tak ważna w korporacjach oraz jak krok po kroku zbudować symulację w Excelu, wykorzystując czyste formuły. Wszystko w formie, którą możesz wdrożyć w swojej praktyce niemal od razu.

Podstawy analizy Monte Carlo
Analiza Monte Carlo opiera się na koncepcji powtarzania obliczeń setki, tysiące, a nawet miliony razy, przy każdym przebiegu losując nowe wartości zmiennych wejściowych. W praktyce oznacza to, że zamiast tworzyć pojedynczą prognozę, generujemy cały „wszechświat” możliwych wyników. Dzięki temu można zobaczyć, jak zmienność poszczególnych parametrów wpływa na ryzyko projektu, przepływy pieniężne czy wycenę przedsiębiorstwa.
Sednem symulacji jest losowość, która zastępuje tradycyjne podejście oparte na jednym zestawie założeń. Monte Carlo pozwala pracować na rozkładach prawdopodobieństwa ale zamiast stwierdzać, że przychody wyniosą 50 mln zł, możemy założyć, że średnio będzie to 50 mln, z odchyleniem standardowym 10 mln, ale rzeczywiste wyniki mogą oscylować między 20 a 80 mln. Z każdym losowaniem powstaje inny scenariusz, a z tysięcy scenariuszy układa się obraz ryzyka, który pozwala podejmować lepsze decyzje.
Różnica między analizą scenariuszową a Monte Carlo jest zasadnicza: scenariusze badają najczęściej trzy punkty (pesymistyczny, realistyczny, optymistyczny), podczas gdy Monte Carlo analizuje pełne kontinuum możliwych stanów. To tak, jakby zamiast zrobić zdjęcie w trzech klatkach, nagrać cały film. Dzięki temu kierownictwo otrzymuje mapę prawdopodobieństw, a nie jedną liczbę oderwaną od ryzyka. W praktyce przekłada się to na większą pewność podejmowania decyzji, mniejszą wrażliwość na błędy założeń oraz bardziej dojrzałe podejście do oceny niepewności.
Monte Carlo bazuje również na fundamentach statystyki, a im więcej iteracji, tym bardziej stabilny staje się rozkład wyników. Dla standardowych zastosowań w finansach korporacyjnych dobrze sprawdza się od 5 tys. do 20 tys. losowań, choć bardziej złożone czy ryzykowne projekty mogą wymagać więcej. Ważne jest także odpowiednie zdefiniowanie zmiennych wejściowych, ich zależności i ograniczeń, a to właśnie w tych miejscach modele najczęściej popełniają błędy.
Dlaczego korporacje stosują Monte Carlo
W dużych organizacjach analiza Monte Carlo stała się jednym z kluczowych narzędzi wykorzystywanych przy podejmowaniu decyzji strategicznych, planowaniu finansowym i ocenie ryzyka inwestycyjnego. Powód jest prosty: korporacje funkcjonują w środowisku pełnym zmiennych, na które mają ograniczony wpływ. Ceny surowców, kursy walut, poziom inflacji, zachowania klientów, stopy procentowe, koszty operacyjne wszystko to może zmieniać się w sposób nieprzewidywalny. Tradycyjne modele finansowe, które zakładają pojedyncze wartości parametrów, są w praktyce zbyt sztywne, by oddać prawdziwą naturę ryzyka. Monte Carlo rozwiązuje ten problem, pozwalając firmom patrzeć na przyszłość z perspektywy prawdopodobieństw, a nie sztywnych prognoz.
W procesie podejmowania decyzji strategicznych Monte Carlo pełni rolę „symulatora lotu” dla menedżerów. Umożliwia sprawdzenie, jak zachowa się model finansowy firmy, gdy kluczowe zmienne ulegną wahaniom czy firma będzie w stanie utrzymać płynność przy niższych niż zakładano przychodach? Czy projekt inwestycyjny pozostanie rentowny, jeśli koszty przekroczą plan o 15%? Zamiast tworzyć jedną prognozę, korporacje otrzymują całą mapę ryzyka, wraz z rozkładem prawdopodobieństw dla kluczowych wskaźników. To pozwala zarządom podejmować decyzje oparte na danych, a nie intuicji.
Jednym z najważniejszych zastosowań Monte Carlo w korporacjach jest modelowanie ryzyka finansowego. Banki, firmy produkcyjne, energetyczne, telekomunikacyjne wszystkie te branże wykorzystują symulacje do badania ekspozycji na zmienność. Przykładowo, firmy energetyczne analizują wpływ wahań cen energii i surowców na marże i przepływy pieniężne, natomiast firmy działające globalnie oceniają ryzyko walutowe, sprawdzając w Monte Carlo, jak zmiany kursów EUR/USD czy USD/PLN odbiją się na wynikach finansowych. Dzięki temu łatwiej jest ustalić limity ryzyka, zabezpieczenia czy poziomy rezerw finansowych.
Korporacje szeroko wykorzystują też Monte Carlo do prognozowania wyników inwestycji szczególnie w analizie NPV, IRR i przepływów pieniężnych projektów. Zamiast przedstawiać zarządowi jedną wartość NPV, analitycy prezentują cały rozkład na przykład: 70% szans, że NPV będzie dodatnie, 20% szans na lekką stratę i 10% szans na całkowitą nieopłacalność projektu. Taki obraz ryzyka jest nieporównywalnie bardziej wartościowy niż pojedyncza liczba.
Monte Carlo pomaga również oceniać odporność budżetów korporacyjnych. Firmy testują swoje plany na zmienność przychodów, kosztów, inflacji czy rotacji pracowników. Dzięki temu możliwe jest określenie, jak stabilny jest budżet, jakie są scenariusze skrajne i gdzie należy zbudować poduszkę bezpieczeństwa. W praktyce oznacza to, że firma może nie tylko przygotować realistyczne cele, ale także odpowiednio zarządzać ryzykiem ich nieosiągnięcia.
Kluczowe elementy modelu Monte Carlo
Aby symulacja Monte Carlo działała poprawnie i dawała wiarygodne wyniki, model musi być zbudowany na solidnych fundamentach. W praktyce oznacza to kilka kluczowych elementów: odpowiednio dobrane zmienne wejściowe, realistyczne rozkłady prawdopodobieństwa, właściwie zdefiniowane zależności oraz odpowiednia liczba iteracji. Brzmi prosto, ale to właśnie te obszary najczęściej decydują o tym, czy model stanie się solidnym narzędziem decyzyjnym, czy jedynie skomplikowaną zabawką w Excelu.
Pierwszym krokiem jest identyfikacja zmiennych wejściowych. W modelach finansowych zwykle są to przychody, marże, ceny materiałów, CAPEX, stopy procentowe, kursy walut czy wolumen sprzedaży. Każda z tych zmiennych wpływa na wynik końcowy, ale nie wszystkie mają taką samą wagę. Dlatego tak ważne jest, aby wybrać tylko te parametry, które faktycznie niosą największą niepewność. Modele przeładowane zmiennymi losowymi stają się nieczytelne i trudne do kalibracji lepiej wybrać kilka kluczowych elementów, ale zdefiniować je precyzyjnie.
Drugim elementem są rozkłady prawdopodobieństwa. To właśnie one decydują, jak zachowają się zmienne w symulacji. Nie wystarczy wpisać „średnia 100, odchylenie 20” trzeba określić, czy dana zmienna podlega rozkładowi normalnemu, log-normalnemu, trójkątnemu czy jednostajnemu. Przykładowo: przychody rzadko mają rozkład normalny, ponieważ nie mogą spaść poniżej zera, ale mogą rosnąć w sposób nieliniowy, dlatego częściej stosuje się rozkład log-normalny. Z kolei koszty inwestycji często opisuje się rozkładem trójkątnym: mamy koszt minimalny, najbardziej prawdopodobny i maksymalny, co tworzy bardziej realistyczny obraz ryzyka.
Kolejnym ważnym elementem są zależności między zmiennymi. W rzeczywistości przychody i koszty nie są od siebie oderwane, a to często wysoka sprzedaż oznacza również większe koszty operacyjne, a wysoka inflacja wpływa zarówno na ceny materiałów, jak i koszty pracy. Modele ignorujące współzależności mogą dawać wyniki zbyt optymistyczne lub zbyt pesymistyczne. Dlatego korporacje często wprowadzają współczynniki korelacji, które wymuszają bardziej realistyczne zachowanie modelu.
Ostatnim elementem jest liczba iteracji. Choć technicznie można przeprowadzić symulację na 500 losowań, w praktyce im więcej, tym lepiej. Modele korporacyjne najczęściej pracują na 5 000–20 000 iteracji, co pozwala wygładzić rozkład wyników i uniknąć efektów losowych. Jeśli liczba iteracji jest zbyt mała, model zaczyna przypominać analizę scenariuszową, a nie o to w Monte Carlo chodzi.
Dobrze zbudowany model Monte Carlo przypomina raczej instrument naukowy niż zwykły arkusz kalkulacyjny: jest logiczny, spójny, oparty na danych i statystycznie stabilny. Dopiero wtedy może stać się narzędziem do podejmowania decyzji na najwyższym poziomie zarządczym.
Najczęściej stosowane rozkłady prawdopodobieństwa
W modelach finansowych rozkłady prawdopodobieństwa odgrywają kluczową rolę, ponieważ to właśnie one decydują o tym, jak zachowają się zmienne w trakcie tysięcy iteracji symulacji. Wybór właściwego rozkładu jest tak samo ważny jak wybór samych zmiennych, a niekiedy nawet ważniejszy. Zastosowanie niewłaściwego rozkładu może prowadzić do wyników całkowicie oderwanych od rzeczywistości. Dlatego analitycy korporacyjni muszą bardzo świadomie podejść do definiowania charakterystyki zmiennych wejściowych. Każdy typ rozkładu niesie bowiem ze sobą specyficzne cechy, które determinują dynamikę otrzymywanych wyników.
Jednym z najpopularniejszych rozkładów jest rozkład normalny, stosowany zwłaszcza w przypadku zmiennych symetrycznych, takich jak odchylenia budżetowe, zmienność kosztów operacyjnych czy zmiana wskaźników makroekonomicznych w krótkim okresie. Rozkład normalny jest wygodny, ponieważ dobrze odzwierciedla naturalne procesy oparte na wielu drobnych zdarzeniach, ale trzeba pamiętać, że dopuszcza wartości ujemne dlatego nie można go stosować do danych, które nie mogą spaść poniżej zera, np. przychodów czy wolumenów sprzedaży.
W takich sytuacjach znacznie lepiej sprawdza się rozkład log-normalny. Ten typ rozkładu pozwala modelować zmienne, które rosną proporcjonalnie i dla których wartości skrajnie wysokie są możliwe, ale niskie mają ograniczenia. Typowymi przykładami są przychody, ceny aktywów, wartości rynkowe czy wzrosty w długich okresach. Rozkład log-normalny ma naturalne zastosowanie w wycenach typu DCF, gdzie przychody i koszty podlegają nie tylko wahaniom, ale również efektom skumulowanym.
Rozkład trójkątny to z kolei ulubione narzędzie menedżerów projektów i działów CAPEX. Dlaczego? Ponieważ pozwala wprost wprowadzić trzy wartości: minimalną, maksymalną oraz najbardziej prawdopodobną. Dzięki temu modelowanie nie wymaga zaawansowanych danych statystycznych, a tu wystarczy wiedza ekspercka. Rozkład trójkątny świetnie sprawdza się do prognozowania kosztów inwestycji, budżetów projektowych czy czasów realizacji. To właśnie ten rozkład najczęściej stosuje się w analizach ryzyka kosztów budowy, modernizacji czy implementacji systemów IT.
Rozkład jednostajny jest najprostszy, ale równocześnie bardzo użyteczny. Zakłada on, że każda wartość w określonym przedziale jest równie prawdopodobna. Choć brzmi to nieskomplikowanie, korporacje stosują ten rozkład m.in. w modelowaniu niepewności wczesnych etapów projektów, przy braku danych historycznych albo do testowania „neutralnych” przedziałów ryzyka. Rozkład jednostajny jest też często wykorzystywany jako baza do tworzenia bardziej złożonych rozkładów za pomocą funkcji warunkowych.
Wybór właściwego rozkładu nie jest kwestią estetyki, lecz fundamentem wiarygodności całego modelu Monte Carlo. Dobre dopasowanie rozkładu do rzeczywistej natury danej zmiennej sprawia, że model zaczyna naśladować świat realny, a wyniki stają się solidnym źródłem wniosków dla zarządu. W praktyce firmy łączą różne rozkłady w jednym modelu, co pozwala precyzyjnie odwzorować złożoność otoczenia biznesowego.
Zastosowania Monte Carlo w finansach korporacyjnych
Symulacja Monte Carlo jest stosowana w korporacjach na ogromną skalę, ponieważ pozwala przełożyć niepewność na konkretne liczby, prawdopodobieństwa i przedziały ryzyka. W praktyce staje się narzędziem, które pozwala podejmować decyzje bardziej świadomie, zamiast polegać na pojedynczej prognozie oderwanej od rzeczywistości. W dużych firmach Monte Carlo wykorzystuje się zarówno w codziennych analizach budżetowych, jak i w wielomilionowych projektach inwestycyjnych, restrukturyzacjach czy wycenach rynkowych.
Jednym z głównych obszarów zastosowania Monte Carlo jest planowanie kapitałowe (CAPEX). Korporacje inwestują w fabryki, linie produkcyjne, centra logistyczne, projekty IT czy systemy automatyzacji, a każdy z tych projektów niesie ze sobą niepewność związaną z kosztami, czasem realizacji i przyszłymi efektami finansowymi. Tradycyjne podejście oparte na pojedynczym budżecie jest niemal zawsze błędne, bo w realnym świecie koszty rzadko mieszczą się w planie. Symulacja Monte Carlo pozwala oszacować prawdopodobieństwo przekroczenia budżetu, określić potrzebny bufor finansowy oraz wskazać, które elementy projektu są najbardziej ryzykowne. Dzięki temu firmy mogą bardziej precyzyjnie zarządzać kapitałem i przygotować się na odchylenia od planu.
NPV (Net Present Value czyli wartość bieżąca netto)
To miara, która pokazuje, ile warta jest inwestycja po zdyskontowaniu wszystkich przyszłych przepływów pieniężnych do wartości dzisiejszej.
Mówiąc prościej: NPV mówi, czy projekt zwraca się po uwzględnieniu kosztu kapitału (stopy dyskontowej).
- Jeśli NPV > 0 – projekt tworzy wartość i jest opłacalny.
- Jeśli NPV < 0 – projekt niszczy wartość i lepiej go nie realizować.
- Jeśli NPV = 0 – projekt wychodzi „na zero”.
To bardzo „zdroworozsądkowa” miara, która sprowadza przyszłość do dzisiejszych warunków i pozwala podjąć decyzję, nie bujając w abstrakcjach.
IRR (Internal Rate of Return to wewnętrzna stopa zwrotu)
To stopa zwrotu projektu, czyli taka wartość procentowa, przy której NPV wychodzi dokładnie 0.
Można na to spojrzeć tak: IRR to „prawdziwa rentowność” projektu, wyrażona w rocznej stopie zwrotu.
- Jeśli IRR > koszt kapitału (np. WACC) – projekt się opłaca.
- Jeśli IRR < koszt kapitału – projekt jest nieatrakcyjny.
IRR jest intuicyjne, bo daje jedną liczbę procentową, ale bywa mylące przy nieliniowych przepływach. Dlatego w korporacjach NPV jest uważane za metodę bardziej profesjonalną i stabilną.
Monte Carlo świetnie sprawdza się również w ocenie projektów inwestycyjnych, a szczególnie tych, które wymagają obliczenia NPV i IRR. Zamiast jednej wartości NPV, korporacje otrzymują cały rozkład wyników, który pokazuje, w ilu procentach przypadków projekt przyniesie zysk, a w ilu zakończy się stratą. Dla zarządów to ogromna różnica: widzą nie tylko średni wynik, ale także ryzyko skrajnych wartości. Modele te są kluczowe w branżach takich jak energetyka, produkcja ciężka, budownictwo, logistyka czy telekomunikacja, wszędzie tam, gdzie koszty i przychody podlegają silnym wahaniom.
W planowaniu budżetów Monte Carlo pozwala testować odporność planów finansowych na zmienność otoczenia. Firmy sprawdzają, jak zmieni się EBITDA, cash flow, marża operacyjna czy zapotrzebowanie na kapitał obrotowy, gdy kluczowe parametry zaczną się wahać. Dzięki temu budżet przestaje być dokumentem oderwanym od rzeczywistości, a staje się narzędziem zarządzania niepewnością. Monte Carlo pozwala określić m.in. ile procent scenariuszy prowadzi do wyniku poniżej oczekiwań oraz ile trzeba zabezpieczyć środków, by przetrwać trudniejsze okresy.
Symulacje są także wykorzystywane w zarządzaniu ryzykiem rynkowym. Firmy narażone na wahania walut, surowców lub stóp procentowych mogą ocenić, jak zmienność tych parametrów wpływa na ich wyniki finansowe. Przykładowo, spółki importujące materiały mogą analizować ekspozycję na USD lub EUR, a przedsiębiorstwa zadłużone oceniają, jak zmiana stóp procentowych wpłynie na koszty finansowe w ciągu najbliższych lat. Monte Carlo pozwala w sposób dynamiczny ocenić, ile firma może stracić lub zyskać w zależności od zmian rynkowych.
Wreszcie, analiza Monte Carlo wspiera analizę wrażliwości. To narzędzie pozwala określić, które zmienne mają największy wpływ na wynik końcowy modelu. Dzięki temu korporacje mogą skoncentrować swoje wysiłki kontrolne na tych obszarach, które generują najwięcej ryzyka. To niezwykle praktyczne podejście, które pozwala uniknąć marnowania zasobów na elementy, które w niewielkim stopniu wpływają na wynik finansowy.
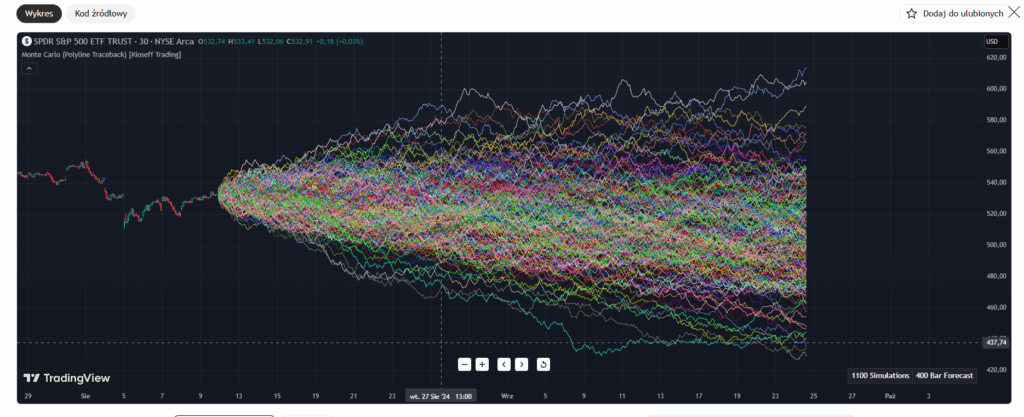
Przedstawiona na wykresie symulacja Monte Carlo pokazuje setki możliwych przyszłych ścieżek cenowych ETF-u SPDR S&P 500 (SPY), wygenerowanych na podstawie historycznej zmienności i zachowania rynku. Każda kolorowa linia reprezentuje jeden potencjalny scenariusz cenowy w kolejnych 400 interwałach, co tworzy charakterystyczny “lejek ryzyka”, ilustrujący narastającą niepewność wraz z upływem czasu. Tego typu wizualizacja pozwala analitykom i inwestorom lepiej zrozumieć pełen rozkład możliwych wyników, zamiast opierać się na pojedynczej, deterministycznej prognozie. Wykres został wygenerowany za pomocą open-source’owego skryptu dostępnego publicznie na TradingView pod adresem: https://pl.tradingview.com/script/L1ZVVqbX-Monte-Carlo-Polyline-Traceback-Kioseff-Trading/. Każdy użytkownik może z niego bezpłatnie korzystać i dowolnie analizować symulacje cenowe.
Monte Carlo w wycenie przedsiębiorstw
Symulacja Monte Carlo stała się jednym z najważniejszych narzędzi wspierających wyceny przedsiębiorstw, szczególnie w metodzie DCF. Tradycyjna wycena DCF opiera się na pojedynczym zestawie prognoz dotyczących przychodów, marż, inflacji, stopy dyskontowej czy nakładów inwestycyjnych. Problem polega na tym, że każda z tych zmiennych obarczona jest znaczną niepewnością, a małe odchylenia w założeniach potrafią wygenerować ogromne różnice w wartości końcowej. Monte Carlo pozwala zamienić tę niepewność w precyzyjnie policzone rozkłady, które znacznie lepiej oddają rzeczywistość.
Pierwszym krokiem w Monte Carlo dla DCF jest zdefiniowanie rozkładów zmiennych kluczowych. Przychody często podlegają rozkładowi log-normalnemu, ponieważ ich zmienność jest asymetryczna, a mogą rosnąć dynamicznie, ale nie mogą spaść poniżej zera. Marże operacyjne mogą być modelowane rozkładem normalnym lub trójkątnym, w zależności od stabilności branży. Stopa dyskontowa z kolei jest zmienną zależną od rynku, więc w korporacjach często modeluje się ją za pomocą rozkładu normalnego lub rozkładów bazujących na danych historycznych. Dzięki zastosowaniu różnych rozkładów dla różnych zmiennych wycena staje się bardziej elastyczna i realistyczna.
W praktyce Monte Carlo sprawia, że otrzymujemy nie jedną wycenę firmy, ale cały wachlarz potencjalnych wartości przedsiębiorstwa, od bardzo niskich po ekstremalnie wysokie. Rozkład wartości przedsiębiorstwa (EV) jest znacznie bardziej informacyjny niż pojedyncza liczba. Zarządy i inwestorzy mogą sprawdzić, jakie jest prawdopodobieństwo, że EV przekroczy określony poziom lub stanie się niższa od oczekiwań. Często przedstawia się histogram wartości wraz z kluczowymi percentylami, takimi jak P5, P50 i P95, dającymi pełny obraz ryzyka i szans.
Monte Carlo jest szczególnie przydatne w sytuacjach, gdy firma funkcjonuje w otoczeniu wysokiej zmienności, na przykład w energetyce, IT, nowych technologiach czy branżach kapitałochłonnych, gdzie przyszłe wyniki mogą diametralnie różnić się od prognoz. Dodatkowo, dzięki symulacjom możliwe jest dokładniejsze określenie wartości opcji realnych, takich jak możliwość odłożenia projektu, jego rozszerzenia czy porzucenia. Tradycyjne podejścia DCF zazwyczaj ignorują te opcje, podczas gdy Monte Carlo pozwala je policzyć w sposób zbliżony do wyceny opcji finansowych.
Wyceny oparte na Monte Carlo dają również większą przejrzystość w procesach fuzji i przejęć. Kupujący oraz sprzedający mogą lepiej zrozumieć ryzyka powiązane z prognozami. To szczególnie ważne przy negocjacjach cenowych, strony widzą, gdzie leży prawdopodobieństwo skrajnych wyników, jak bardzo projekty synergiowe są niepewne oraz jak wygląda rzeczywista ekspozycja na czynniki rynkowe. Co więcej, Monte Carlo pozwala zidentyfikować te zmienne, które najbardziej wpływają na wartość przedsiębiorstwa, co z kolei ułatwia planowanie działań strategicznych czy optymalizacyjnych po przejęciu.
Ostatecznie Monte Carlo sprawia, że wycena przestaje być statycznym dokumentem, a staje się żywym narzędziem, które można aktualizować wraz ze zmianą danych rynkowych. Daje również firmom przewagę konkurencyjną, ponieważ pozwala podejmować decyzje oparte na pełnym spektrum możliwych scenariuszy, a nie tylko na jednym, najbardziej prawdopodobnym.
Budowanie modelu Monte Carlo w Excelu
Budowa modelu Monte Carlo w Excelu może wydawać się zadaniem skomplikowanym, ale w rzeczywistości opiera się na jasnej, powtarzalnej strukturze. Korporacje wykorzystują Excel, ponieważ jest on narzędziem dostępnym, elastycznym i wystarczająco potężnym, by przeprowadzić nawet kilkadziesiąt tysięcy iteracji, o ile model jest odpowiednio skonstruowany. Fundamentem pracy w Excelu jest rozdzielenie zmiennych wejściowych, sekcji losowania oraz wyników końcowych. Dzięki temu model pozostaje przejrzysty, a analityk może w łatwy sposób zmieniać założenia bez ryzyka zaburzenia struktury.
Pierwszym krokiem jest podzielenie arkusza na logiczne sekcje. Często stosuje się trzy główne obszary: założenia (np. średnie wartości, odchylenia, minima i maksima), sekcję losowań (gdzie Excel generuje zmienne losowe na podstawie rozkładów) oraz część obliczeniową, w której liczony jest NPV, cash flow, EBITDA czy inny wskaźnik. Taki układ nie tylko ułatwia orientację, ale również minimalizuje ryzyko błędów. Dobrą praktyką jest także kolorowanie komórek, na przykład niebieskie dla założeń, zielone dla losowań i czarne dla formuł wynikowych.
Następnym elementem jest zdefiniowanie zmiennych losowych. W Excelu nie ma wbudowanych generatorów rozkładów prawdopodobieństwa (chyba że korzystamy z dodatków), dlatego rozkłady trzeba odtworzyć ręcznie przy użyciu funkcji takich jak RAND, RANDBETWEEN oraz funkcji INVERSE do rozkładów statystycznych. Przykładowo, rozkład normalny można wygenerować, stosując formułę NORM.INV(RAND(); średnia; odchylenie). Dla rozkładu trójkątnego stosuje się formuły IF, które zależnie od wartości losowej RAND generują minimum, maksimum lub wartość najbardziej prawdopodobną.
Ważnym elementem budowy modelu jest również powiązanie zmiennych z modelem finansowym. Losowania muszą bezpośrednio wpływać na obszar wyników, np. na przychody w każdym roku, koszty operacyjne czy poziomy inwestycji. W ten sposób każda iteracja modelu jest kompletną „ucieczką do świata alternatywnego”, w którym wszystkie parametry zmieniają się losowo, zgodnie z wcześniej zdefiniowanymi zasadami. Dopiero wtedy model zaczyna działać jak prawdziwa symulacja.
Kluczową decyzją jest także wybór liczby iteracji. Excel jest narzędziem ograniczonym pod względem wydajności, ale dobrze zaprojektowany model poradzi sobie nawet z 20 000 losowań. Najczęściej iteracje buduje się w formie wierszy, gdzie każdy wiersz to jedna symulacja: Excel losuje zmienne, przepuszcza je przez formuły modelu i zapisuje wynik końcowy. Im więcej takich wierszy, tym bardziej stabilny i realistyczny staje się rozkład wyników.
Dobrą praktyką jest także dodanie elementów kontrolnych: blokady przypadkowych zmian, nazw formuł, sprawdzania zakresów, walidacji danych. Modele Monte Carlo w korporacjach często są przeglądane przez kilka osób, audytorów, kontrolerów, menedżerów, więc jasna struktura eliminuje nieporozumienia. Ważne jest również, aby każdy element modelu był opisany i udokumentowany, ponieważ Monte Carlo jest narzędziem analitycznym, ale musi pozostać zrozumiałe dla osób, które nie budowały go samodzielnie.
Z pozoru Excel jest prostym narzędziem, ale odpowiednio wykorzystany staje się potężnym silnikiem do symulacji. Wymaga to jedynie dobrej struktury, spójnych założeń oraz konsekwencji w stosowaniu logiki. Gdy te elementy są spełnione, model Monte Carlo może działać na bardzo wysokim poziomie, porównywalnym z dedykowanymi narzędziami wykorzystywanymi w korporacjach finansowych.
Symulacja Monte Carlo w Excelu bez dodatków
Choć w świecie korporacyjnym istnieje wiele zaawansowanych dodatków i narzędzi do statystyki, bardzo często analitycy, z różnych powodów i muszą pracować wyłącznie na „czystym” Excelu. Dobrze zbudowana symulacja Monte Carlo może działać perfekcyjnie nawet bez jakichkolwiek wtyczek. Kluczem jest umiejętne posługiwanie się funkcjami RAND, RANDBETWEEN oraz funkcjami odwrotnymi rozkładów (INVERSE). Wszystko sprowadza się do jednego: generowania losowych wartości zgodnie z określoną charakterystyką.
Najprostszą metodą jest użycie funkcji RAND, która generuje liczbę z przedziału od 0 do 1. To właśnie ona staje się „ziarnem losowości”, które potem można przekształcić w dowolny rozkład. RAND jest podstawą większości symulacji, ponieważ daje równomiernie rozłożone wyniki, które można następnie przepuścić przez formuły generujące rozkłady normalne, log-normalne czy trójkątne. Jeśli potrzebne są wartości całkowite, stosuje się RANDBETWEEN to świetny do prostych modeli z rozkładem jednostajnym.
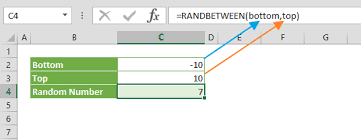
W praktyce budowanie symulacji zaczyna się od stworzenia sekcji, w której Excel wygeneruje np. 10 000 zestawów wartości losowych. Każdy zestaw reprezentuje jedną iterację symulacji. W jednym wierszu mogą znajdować się np. przychody, koszty, marża, CAPEX, a na końcu formuła licząca NPV lub wynik finansowy. Excel automatycznie przeliczy każdą komórkę przy każdym odświeżeniu arkusza i to dzięki czemu powstaje potężny silnik symulacyjny, działający wyłącznie na formułach.
Jeśli chcemy wygenerować rozkład normalny, stosujemy funkcję NORM.INV, która „tłumaczy” wartość losową RAND na wartość zgodną z rozkładem normalnym. To dokładnie tak, jakbyśmy brali jednolity los i przepuszczali go przez „filtr statystyczny”, który zamienia go w los zgodny z rozkładem normalnym. Dla bardziej złożonych rozkładów, takich jak trójkątny, konieczne jest użycie funkcji IF, aby odpowiednio „podzielić” zakres losowy i przyporządkować go do odpowiednich przedziałów wartości.
Kluczowym aspektem jest również sposób wykonania iteracji. Najczęściej buduje się kolumny losowań w dół arkusza, gdzie każdy wiersz to osobny przebieg symulacji. W praktyce oznacza to, że Excel w jednej kolumnie losuje np. przychody, w drugiej koszty, w trzeciej marżę, w czwartej CAPEX, a w piątej liczy wynik końcowy. Dzięki temu możemy w szybki sposób stworzyć dużą próbę wyników, którą później analizujemy np. tworząc histogramy, licząc percentyle czy wyciągając scenariusze skrajne.
W symulacji Monte Carlo w Excelu ważne jest również optymalizowanie wydajności. RAND odświeża się za każdym razem, gdy arkusz oblicza się ponownie, co może powodować duże obciążenie przy tysiącach wierszy. Dlatego dobrą praktyką jest wklejenie wyników jako wartości w osobnej sekcji, w ten sposób zamrażamy losowania i możemy bezpiecznie pracować na danych, bez ryzyka przypadkowych zmian. Korporacje często stosują też makra do automatycznego generowania i zamrażania losowań, ale nie jest to konieczne, sam Excel w zupełności wystarcza.
Symulacja bez dodatków jest w pełni funkcjonalna i daje wyniki porównywalne z profesjonalnymi narzędziami. Warunkiem jest konsekwentne stosowanie formuł i logiczna struktura arkusza. Excel, choć pozornie prosty, potrafi stać się potężnym narzędziem analitycznym, jeśli wykorzystać jego funkcje w sposób przemyślany i uporządkowany.
Najczęstsze formuły używane przy budowie rozkładów
Budowanie rozkładów prawdopodobieństwa w Excelu bez dodatków wymaga świadomego wykorzystania kilku kluczowych funkcji. To one pozwalają przekształcić losową liczbę z funkcji RAND w wartości zachowujące się zgodnie z charakterystyką danego rozkładu. Dobrze skonstruowany zestaw formuł umożliwia stworzenie realistycznych zmiennych wejściowych, które później wpływają na wyniki symulacji Monte Carlo. W praktyce te formuły stają się sercem całego modelu, to one decydują, czy symulacja będzie wiarygodna, stabilna i zgodna z rzeczywistością.
Najbardziej klasycznym przypadkiem jest rozkład normalny. Excel umożliwia jego generowanie za pomocą funkcji NORM.INV. To funkcja odwrotna dystrybuanty, która zamienia jednolity los z RAND na wartość zgodną z rozkładem normalnym o zadanej średniej i odchyleniu standardowym. Typowa formuła wygląda tak:=NORM.INV(RAND(); Średnia; Odchylenie).
Dzięki temu otrzymujemy zmienną symetryczną, najczęściej używaną przy kosztach operacyjnych, inflacji, odchyleniach budżetowych czy krótkoterminowych wskaźnikach rynkowych. To jedna z najbardziej eleganckich i jednocześnie praktycznych metod na tworzenie realistycznych zmiennych.
Rozkład trójkątny wymaga nieco większej kreatywności. Excel nie ma gotowej funkcji generującej ten rozkład, dlatego trzeba go zbudować ręcznie. Najczęściej stosuje się podejście oparte na funkcji IF, które dzieli zakres RAND na dwie części: wzrostową i spadkową. Przykładowo, jeśli mamy wartości: minimum, maksimum i najbardziej prawdopodobną, rozkład tworzy się za pomocą sekwencji logicznej, która określa, czy losowanie trafia na lewą czy prawą stronę trójkąta. Efekt końcowy jest bardzo zbliżony do prawdziwego rozkładu trójkątnego, który często stosuje się w modelach CAPEX, budżetach projektowych czy analizach czasu realizacji zadań.
Rozkład log-normalny z kolei świetnie nadaje się do modelowania zmiennych, które mogą rosnąć w sposób wykładniczy, ale nigdy nie spadają poniżej zera, jak przychody, ceny aktywów czy długookresowe zmiany wartości rynkowych. Matematycznie log-normalny powstaje przez przekształcenie rozkładu normalnego za pomocą funkcji wykładniczej. W Excelu można go uzyskać w prosty sposób: =EXP(NORM.INV(RAND(); Średnia; Odchylenie)). Ten typ rozkładu jest niezwykle popularny w finansach korporacyjnych, ponieważ bardzo dobrze oddaje asymetryczność ryzyka, możliwe są duże wzrosty, ale spadki są ograniczone.
Rozkład jednostajny jest najprostszy do wygenerowania, wystarczy funkcja RANDBETWEEN dla wartości całkowitych lub kombinacja RAND z mnożeniem i dodaniem dla wartości ciągłych. Ten rozkład świetnie sprawdza się w sytuacjach, gdzie brakuje danych historycznych lub gdy chcemy uniknąć uprzedzeń dotyczących tego, która wartość jest bardziej prawdopodobna. Jest często stosowany przy wczesnych analizach projektowych, modelowaniu niepewności kosztów w pierwszych fazach inwestycji oraz przy budowaniu zestawów testowych.
Warto zwrócić uwagę, że formuły w Excelu należy nie tylko umieć napisać, ale także świadomie interpretować. Każdy rozkład ma inną charakterystykę, a złe dopasowanie może prowadzić do błędnych wniosków. Dlatego w korporacyjnych modelach Monte Carlo często stosuje się kombinacje rozkładów, zależności między zmiennymi oraz kalibracje oparte na danych historycznych. Dzięki temu symulacje stają się narzędziem nie tylko dokładnym, ale przede wszystkim wiarygodnym i praktycznym.
Wykonanie tysięcy iteracji w Excelu
Przeprowadzenie tysięcy iteracji w Excelu to kluczowy element symulacji Monte Carlo, to właśnie liczba przebiegów decyduje o wiarygodności rozkładu wyników. Wbrew pozorom Excel radzi sobie z tym zadaniem zaskakująco dobrze, o ile model jest prawidłowo zorganizowany i zoptymalizowany. Podejście stosowane w korporacjach polega na tworzeniu dużej tabeli, w której każdy wiersz reprezentuje jedną pełną symulację: losowanie wszystkich zmiennych wejściowych oraz obliczenie wyniku końcowego, np. NPV, EBITDA, CAPEX czy cash flow.
EBITDA (Earnings Before Interest, Taxes, Depreciation and Amortization)
Wynik operacyjny firmy przed uwzględnieniem:
- odsetek,
- podatków,
- amortyzacji i umorzenia.
Pokazuje realną zdolność firmy do generowania gotówki z działalności operacyjnej, to często stosowany przy wycenie przedsiębiorstw i ocenie rentowności.
CAPEX (Capital Expenditures – nakłady inwestycyjne)
Wydatki na zakup, modernizację lub budowę aktywów trwałych, takich jak:
- maszyny,
- linie produkcyjne,
- nieruchomości,
- infrastruktura IT.
CAPEX to inwestycje długoterminowe, które zwiększają przyszłą wartość firmy, ale obciążają gotówkę w momencie poniesienia.
Pierwszym krokiem jest przygotowanie bloków losowań, zwykle w formie oddzielnych kolumn. Jedna kolumna generuje przychody, druga koszty, trzecia kurs walutowy, czwarta marżę, piąta CAPEX itd. Każda z tych kolumn korzysta z rozkładów zbudowanych wcześniej, czyli z formuł opartych na RAND, RANDBETWEEN, NORM.INV czy konstrukcjach IF dla rozkładu trójkątnego. Dzięki temu po skopiowaniu wiersza w dół Excel automatycznie tworzy tysiące nowych, unikalnych kombinacji wartości.
Następnie w ostatniej kolumnie buduje się formułę wyniku, w zależności od modelu może to być zysk netto, NPV projektu, wolne przepływy pieniężne lub dowolna inna metryka. Tutaj Excel działa jak „silnik”: bierze wylosowane zmienne i przelicza je przez model finansowy, tak jakby każda iteracja była osobnym światem z alternatywnymi wartościami rynkowymi. W efekcie powstaje pełen zestaw wyników, który później staje się podstawą analizy ryzyka.
Największym wyzwaniem jest obciążenie procesora. Excel potrafi liczyć setki tysięcy formuł w czasie rzeczywistym, ale jeśli zbudujemy model nieoptymalnie, arkusz zacznie działać wolno. Dlatego najlepszą praktyką jest oddzielenie części losowej od części obliczeniowej, Excel wtedy nie powtarza niepotrzebnie tych samych obliczeń. Innym popularnym rozwiązaniem jest kopiowanie wyników jako wartości po przeprowadzeniu symulacji, zamraża to dane i pozwala na analizę bez ciągłego przeliczania.
W korporacjach stosuje się też tzw. iteracje blokowe: zamiast liczyć 10 tys. wierszy na raz, analityk generuje np. 1000 losowań, kopiuje wartości, zapisuje je w innym arkuszu, a następnie powtarza proces wielokrotnie. Pozwala to odciążyć Excel i zapewnia stabilność obliczeń. W niektórych firmach wykorzystuje się makra VBA, które automatyzują ten proces, choć nie jest to konieczne, bardzo usprawnia pracę przy dużych modelach.
Na końcu powstaje ogromna baza wyników, którą można analizować statystycznie. To właśnie ta baza nadaje symulacji sens: im większa liczba iteracji, tym bardziej „gładki” i wiarygodny staje się rozkład. Excel, przy właściwej strukturze, z łatwością radzi sobie z setkami tysięcy losowań, sprawiając, że Monte Carlo staje się narzędziem dostępnym praktycznie dla każdego analityka.
Analiza wyników symulacji
Gdy model wygeneruje już tysiące lub nawet dziesiątki tysięcy iteracji, zaczyna się najważniejsza część całego procesu Monte Carlo, interpretacja wyników. To właśnie analiza rozkładu końcowych wartości pozwala zrozumieć, jak duże jest ryzyko danego projektu, budżetu czy całej firmy. W korporacjach to etap, który trafia na biurka dyrektorów, członków zarządów czy komitetów inwestycyjnych. Tam nie chodzi o same liczby, chodzi o decyzje, które opierają się na solidnych, statystycznych fundamentach.
Najczęściej pierwszym krokiem jest stworzenie histogramu wyników. Histogram pozwala szybko zobaczyć, jak rozkładają się wartości końcowe, czy są symetryczne, czy mocno przesunięte, czy istnieją ogony, które sygnalizują ryzyka skrajne. Excel świetnie radzi sobie z tworzeniem histogramów za pomocą wbudowanych narzędzi wykresów. W praktyce histogram zaczyna być „wizualną mapą ryzyka”, którą łatwo interpretują nawet osoby bez wiedzy statystycznej. Jeżeli większość wyników gromadzi się powyżej zera, projekt ma dużą szansę powodzenia. Jeśli poniżej,ryzyko jest wyraźne.
Drugim kluczowym elementem analizy są percentyle. W badaniach finansowych najczęściej używa się P5, P50 i P95. P5 oznacza wynik, poniżej którego znajduje się tylko 5% najgorszych scenariuszy. P50 to mediana, najbardziej reprezentatywna wartość scenariusza „środkowego”. P95 pokazuje natomiast, jaki poziom wyniku osiąga 5% najlepszych symulacji. Ten zestaw trzech liczb daje szybki i kompletny obraz: pokazuje, ile można stracić, jaki jest wynik typowy i jakie są potencjalne korzyści. W Excelu percentyle liczy się za pomocą funkcji PERCENTILE.EXC lub PERCENTILE.INC, zależnie od preferowanego podejścia.
Kolejną praktyczną techniką jest analiza przedziałów ryzyka. Polega ona na określeniu prawdopodobieństwa, że wynik znajdzie się w określonym zakresie. Na przykład: „Istnieje 72% szans, że NPV będzie dodatnie” albo „Ryzyko przekroczenia budżetu o więcej niż 15% wynosi 18%”. Takie komunikaty są niezwykle czytelne dla zarządów, ponieważ pozwalają na podejmowanie decyzji nie na podstawie intuicji, ale twardych danych. Excel umożliwia policzenie udziałów procentowych w bardzo prosty sposób, wystarczy policzyć liczbę wierszy spełniających warunek i podzielić ją przez liczbę wszystkich scenariuszy.
W analizie Monte Carlo ogromną rolę odgrywają również wykresy: wykresy gęstości, box-ploty czy wykresy kumulacyjne (CDF). Wizualizacja wyników sprawia, że nawet skomplikowane rozkłady stają się intuicyjne i łatwe do interpretacji. Na przykład wykres CDF świetnie obrazuje, jak rośnie prawdopodobieństwo uzyskania wyniku powyżej określonego progu. To potężne narzędzie wspierające decyzje strategiczne.
W praktyce korporacyjnej analiza wyników obejmuje także identyfikację zmiennych, które mają największy wpływ na wynik końcowy. Wykorzystuje się do tego analizę korelacji albo tzw. tornado chart. Pozwala to wskazać, które parametry wymagają lepszego zarządzania, zabezpieczeń lub dodatkowych danych. To jeden z najcenniejszych efektów Monte Carlo, wskazuje, które elementy modelu generują najwięcej ryzyka i gdzie organizacja powinna skoncentrować swoje działania.
Analiza wyników symulacji nie polega tylko na patrzeniu na liczby, chodzi o zrozumienie dynamiki ryzyka, jego kierunku i jego możliwych skutków. Monte Carlo pozwala przełożyć niepewność na język, który jest zrozumiały, klarowny i użyteczny biznesowo. Dzięki temu organizacje mogą podejmować decyzje świadome, oparte na probabilistycznych modelach rzeczywistości.
Najczęstsze błędy w modelach Monte Carlo
Mimo że sama koncepcja Monte Carlo wydaje się przejrzysta, to w praktyce wiele modeli korporacyjnych zawiera błędy, które potrafią całkowicie zniekształcić wyniki. Co ciekawe, nie wynikają one z braku umiejętności korzystania z Excela, lecz z braku właściwego podejścia do statystyki, logiki oraz zrozumienia mechaniki samej symulacji. W efekcie modele wyglądają profesjonalnie, mają rozbudowane formuły, wykresy i setki iteracji, ale de facto nie oddają prawdziwego ryzyka. W świecie korporacyjnym takie błędy mogą prowadzić do błędnych decyzji inwestycyjnych, niedoszacowania kosztów lub budżetów, a nawet do nieprawidłowej wyceny projektów czy całych przedsiębiorstw.
Jednym z najczęstszych błędów jest stosowanie niewłaściwych rozkładów prawdopodobieństwa. Wielu analityków automatycznie używa rozkładu normalnego, często dlatego, że jest łatwy do wygenerowania i dobrze znany. Problem polega na tym, że normalny rozkład nie nadaje się do modelowania zmiennych, które nie mogą mieć wartości ujemnych, takich jak przychody, wolumeny czy ceny. W rezultacie powstają symulacje, w których Excel losuje wartości nierealne, a to z kolei zaburza rozkład wyników i prowadzi do błędnej interpretacji. Niektóre modele dopuszczają nawet ujemne koszty, co oczywiście nie ma sensu.
Drugim powszechnym problemem jest ignorowanie zależności pomiędzy zmiennymi. W rzeczywistości większość parametrów ekonomicznych i finansowych jest ze sobą powiązana, wyższa sprzedaż zwykle wiąże się z wyższymi kosztami operacyjnymi, wzrost inflacji może wpływać jednocześnie na przychody i koszty, a zmiana kursów walut często koreluje z cenami surowców. Jeśli model Monte Carlo losuje każdą zmienną niezależnie, powstają kombinacje nierealistyczne, np. wysoka sprzedaż przy bardzo niskich kosztach, albo wysokie koszty przy niskim wolumenie. Wyniki takich symulacji są pozornie precyzyjne, ale całkowicie mijają się z realiami biznesowymi.
Kolejnym często spotykanym błędem jest zbyt mała liczba iteracji. Symulacja Monte Carlo opiera się na prawie wielkich liczb , im więcej losowań, tym bardziej stabilny staje się rozkład wyników. Jeśli model ma tylko 200 lub 300 iteracji, rozkład będzie pełen przypadkowych pików, a percentyle staną się niestabilne i mylące. W praktyce korporacyjnej za minimum uważa się 5 000 iteracji, a dla projektów o dużej zmienności stosuje się nawet 20 000. Niestety wielu analityków robi modele z kilkuset iteracji, bo Excel zaczyna działać wolno, co świadczy o słabej optymalizacji, a nie o ograniczeniach narzędzia.
Częstym błędem jest także brak walidacji danych wejściowych. Monte Carlo nie jest magiczną metodą, która naprawia złe założenia, przeciwnie, jeśli dane wejściowe są błędne, symulacja tylko powiela te błędy tysiące razy. Dlatego tak ważne jest oparcie się na twardych danych: analizach historycznych, benchmarkach rynkowych, danych makroekonomicznych czy opiniach ekspertów. Modele bez walidacji są nie tylko bezużyteczne, ale mogą wprowadzać firmę w poważne ryzyko.
Poważnym problemem jest również nadmierna komplikacja modeli. Wiele korporacyjnych modeli Monte Carlo jest przeładowanych zmiennymi, które w rzeczywistości mają znikomy wpływ na wynik. Zbyt skomplikowany model staje się nieprzejrzysty i trudny do aktualizacji. Prawdziwa sztuka polega na uproszczeniu, skupieniu się na kilku zmiennych, które faktycznie kształtują wynik modelu.
Na końcu pojawia się błąd interpretacyjny, analitycy skupiają się na średniej wyników zamiast na pełnym rozkładzie. Tymczasem największą wartością Monte Carlo jest analiza ryzyka: ogonów rozkładu, prawdopodobieństw skrajnych scenariuszy i przedziałów ufności. Średnia bywa myląca, szczególnie gdy rozkład jest asymetryczny.
Unikanie tych błędów sprawia, że model Monte Carlo staje się narzędziem nie tylko dokładnym, ale przede wszystkim praktycznym. A w finansach korporacyjnych chodzi właśnie o praktyczność, wiarygodność i możliwość podejmowania trafnych decyzji.
Przykład praktyczny: projekt inwestycyjny
Aby zrozumieć, jak Monte Carlo działa w praktyce, najlepiej przejść przez kompletny przykład, taki, jaki przygotowują analitycy finansowi w korporacjach przy ocenie projektów inwestycyjnych. Przykład oparty jest na klasycznym zadaniu: oszacowaniu NPV projektu, którego wyniki są obarczone niepewnością. W prawdziwym świecie rzadko kiedy znamy dokładne przyszłe przychody, koszty operacyjne czy poziom inwestycji, zmienność jest normą, a nie wyjątkiem. Monte Carlo pozwala oszacować nie tylko jedną wartość NPV, ale całą mapę ryzyka projektu.
Załóżmy, że firma planuje inwestycję w nową linię produkcyjną. W tradycyjnym modelu analityk przygotowałby prognozę przychodów, kosztów i przepływów pieniężnych, a następnie policzył NPV. Jednak w rzeczywistości dane są niepewne:
- Przychody mogą wynosić od 18 mln do 30 mln zł, z wartością najbardziej prawdopodobną na poziomie 24 mln.
- Koszty operacyjne wahają się od 9 mln do 13 mln zł, najczęściej utrzymując się w okolicy 11 mln.
- CAPEX wynosi od 35 mln do 45 mln zł, z najbardziej prawdopodobnym kosztem 40 mln.
- Stopa dyskontowa ma średnią 9% i odchylenie 1,5%.
To typowy zestaw zmiennych dla projektu inwestycyjnego, każda z nich ma naturalną zmienność i każda wpływa na NPV. W Excelu można je łatwo przekształcić w rozkłady. Przychody i koszty modeluje się najczęściej rozkładem trójkątnym, a stopę dyskontową rozkładem normalnym. Każda iteracja modelu generuje nową kombinację wartości i nową wartość NPV.
W praktycznej symulacji analityk tworzy tabelę z tysiącami wierszy, gdzie każdy wiersz to pełna symulacja: Excel losuje przychody, koszty, CAPEX i stopę dyskontową, następnie przepuszcza je przez wzór na NPV i zapisuje wynik. Po wykonaniu 10 tys. iteracji powstaje bogaty zbiór danych, rozkład końcowych wartości NPV. Zamiast jednej liczby pojawia się pełny obraz ryzyka projektu.
W analizie wyników mogą pojawić się następujące wnioski:
- 67% symulacji daje NPV dodatnie, projekt ma więc więcej szans na sukces niż porażkę.
- Mediana NPV wynosi 4,8 mln zł, oznacza to, że typowy wynik projektu jest pozytywny.
- W P5 NPV osiąga –12 mln zł, ryzyko poważnej straty jest niskie, ale istnieje.
- W P95 NPV osiąga ponad 18 mln zł, czyli w najlepszych 5% scenariuszy projekt jest wyjątkowo zyskowny.
Dzięki temu zarząd może ocenić projekt nie tylko przez pryzmat średniego wyniku, ale całego spektrum ryzyka. Przykład ten pokazuje, jak bardzo Monte Carlo zmienia proces decyzyjny, zamiast pytać: „Ile wynosi NPV?”, można zapytać: „Jakie jest prawdopodobieństwo, że ten projekt się opłaci?”. A to zupełnie inny poziom analizy.
Monte Carlo pozwala więc spojrzeć na projekt szerzej: gdzie leży ryzyko, jakie są możliwe zyski, co może pójść dobrze, a co źle. To właśnie dlatego korporacje uwzględniają tę metodę w procesach inwestycyjnych, zarządzaniu kapitałem oraz w ocenie długoterminowych planów rozwojowych.
Podsumowanie roli Monte Carlo w finansach korporacyjnych
Symulacja Monte Carlo stała się jednym z najważniejszych narzędzi nowoczesnej analizy finansowej w korporacjach. Jej największą siłą jest to, że pozwala zastąpić pojedyncze prognozy pełnym spektrum możliwych wyników, uwzględniając niepewność, zmienność i ryzyko, które są naturalnym elementem każdej decyzji finansowej. Dzięki Monte Carlo organizacje przestają patrzeć na przyszłość w sposób deterministyczny, zaczynają myśleć probabilistycznie. To zaś prowadzi do podejmowania decyzji bardziej odważnych, ale też bardziej świadomych.
W praktyce Monte Carlo daje korporacjom potężny zestaw narzędzi: od oceny projektów inwestycyjnych, przez budżetowanie i planowanie strategiczne, aż po wycenę przedsiębiorstw. Pozwala budować scenariusze nie tylko najbardziej prawdopodobne, ale także skrajnie pesymistyczne i skrajnie optymistyczne, co ułatwia zarządzanie ryzykiem i przygotowywanie odpowiednich buforów finansowych. Dzięki temu zarządy zyskują klarowny obraz tego, jak firma zachowa się w różnych warunkach, nie tylko w tych, które są najbardziej realne, ale również w tych, które są najbardziej niebezpieczne.
Monte Carlo jest też narzędziem bardzo praktycznym. Można je wdrożyć w Excelu bez dodatków, za pomocą kilku przemyślanych formuł i dobrze zorganizowanego arkusza. Pozwala to analitykom w każdej firmie tworzyć zaawansowane modele, które wcześniej wymagałyby dedykowanego oprogramowania. Oczywiście dobre symulacje wymagają właściwych założeń, prawidłowego doboru rozkładów, odpowiedniej liczby iteracji i zrozumienia zależności między zmiennymi. Jednak dobrze zbudowany model daje ogromną przewagę informacyjną, i to przewagę, którą można wykorzystać od razu.
Ostatecznie Monte Carlo jest metodą, która nie tyle przewiduje przyszłość, ile opisuje jej możliwe ścieżki. W świecie niepewności to właśnie taki sposób myślenia staje się kluczowy. Zamiast pytać „co się stanie?”, korporacje zaczynają pytać „co może się stać, i z jakim prawdopodobieństwem?”. To pytanie otwiera drogę do znacznie bardziej świadomego zarządzania finansami, ryzykiem i strategią.
FAQ
- Czy Excel wystarczy do przeprowadzenia symulacji Monte Carlo?
Tak, Excel w zupełności wystarcza. Wykorzystując funkcje RAND, NORM.INV oraz złożone formuły logiczne, można stworzyć rozbudowane i w pełni funkcjonalne symulacje. - Ile iteracji powinno się wykonywać w modelu Monte Carlo?
Minimalnie 5 000, a najlepiej 10 000–20 000 iteracji. Przy mniejszej liczbie wyniki będą niestabilne i mniej wiarygodne. - Jaki rozkład najlepiej nadaje się do modelowania przychodów?
Najczęściej stosuje się rozkład log-normalny lub trójkątny przychody są asymetryczne i nie mogą spaść poniżej zera. - Czy Monte Carlo można stosować do wyceny przedsiębiorstwa?
Jak najbardziej. Monte Carlo wnosi ogromną wartość do wycen DCF, ponieważ pokazuje rozkład możliwych wartości przedsiębiorstwa, a nie tylko jedną liczbę. - Jakie są najczęstsze błędy w modelach Monte Carlo?
Złe dopasowanie rozkładów, ignorowanie zależności między zmiennymi, zbyt mała liczba iteracji oraz brak walidacji danych wejściowych.